How to Construct a Perfect Octagon

In World War II, my father was a Chief Carpenter's Mate in the Sea Bees (Construction Batallion) on Saipan. One day, his crew was assigned to lay out the forms for an octagonal concrete pad for a water tower. The LT, bright young civil engineer that he was, told my father to wait for him to return with the angles and measurements for the form and to not have the crew do anything. Then he left for his office to use his book of trig tables and his slide rule. As soon as he left, my father laid out the pad and put the men to work.

When the LT returned, he was furious, but then as he measured the form he was amazed to find that my father had laid it out perfectly. "How did you do that, Chief?" "Oh, I dunno. Just threw it together. Lucky, I guess."

No, he wasn't just lucky. He knew exactly what he was doing. At the beginning of the war, my father wanted to enlist, but he wasn't allowed to because he worked in the shipyard, a vital defense industry. So in order to enlist, he had to quit his job at the shipyard. While his enlistment was being processed, he still had to support his family, so he work a few jobs, including one in which he made traffic signs. It was while making stop signs there that he learned how to construct a perfect octagon.

And it works for any size of octagon. Without having to calculate any measurements.

The Procedure:

1. Start with a square.
2. Find the center of square by drawing the two diagonals.

Set the span of your compass from one corner to the center.

3. Set the pivot point of the compass in one corner and mark both sides from that corner.
4. Do the same for each of the other three corners.
5. Now each corner has two marks close to it.

For each of the four corners, draw a line segment connecting those two marks with each other.

6. Now for each of the four corners, cut the corner off along that line segment.
7. Now you have a perfect octagon.

The Proof:

Of course, I had to verify that it really works, so I performed a proof. Yes, it does work, of course. Now decades later I've reaccomplished the proof. I won't claim that it's mathematically rigorous -- what with geometry class having been over 30 years ago -- , but it should prove the construction method.
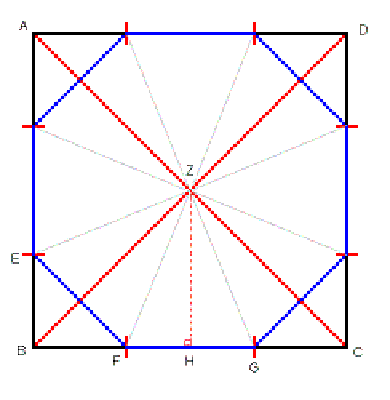
Consider the diagram below in which square ABCD is used to construct an octagon:
From the definition of a regular polygon, we know:
  1. That a regular octagon will contain 8 identical isoceles triangles.

  2. That the internal angle of each triangle -- eg, the angle FZG -- will be one-eighth of a full circle; ie, 360° / 8 = 45°.

  3. That each face of the octagon will be of identical length; eg, the line segments EF and FG.
The approach of the proof will be to demonstrate that all three of these facts hold for the octagon constructed from the square ABCD.

To start with, let's calculate the lengths of the line segments:

  1. Assign the length, s, to the side of the square; eg, line segment AB. Since this is a square, we know that all four sides have the same length, which is s.

  2. The length of the diagonals (AC and BD) are obtained from the Pythagorean Theorem:
    s2 + s2 = AC2
    AC = SQRT(2s2)
    AC = s * SQRT(2)

  3. The compass is set to half the length of a diagonal, therefore to AC/2 or SQRT(2) * s/2 .

  4. The line segments created with the compass are of length SQRT(2)*s/2; eg, AE, BG, CF.

  5. The shorter line segments this creates about each corner (eg, BE, BF) are of length:
    s - SQRT(2)*s/2

  6. The octagon faces that lie on the square (eg, FG) are of length:
    FG = s - 2 * (s - SQRT(2)*s/2)
    FG = s - 2s + SQRT(2)*s
    FG = s * (1 - 2 + SQRT(2))
    FG = s * (SQRT(2) - 1)

  7. Consider now the length of the octagon faces that lie across the square's corners and that are formed by cutting the corners off (eg, EF). This could be determined by applying the Pythagorean Theorem, it turns out that we're dealing with right isoceles triangles again (eg, the triangle BEF), as was the triangle ABC in item #2 above. Thus we already know that the length of segment EF will be BE * SQRT(2). Therefore:
    EF = BE * SQRT(2)
    EF = (s - SQRT(2)*s/2) * SQRT(2) [from item #5]
    EF = s*SQRT(2) - s
    EF = s*SQRT(2) - s
    EF = s * (SQRT(2) - 1)
    EF = FG [from item #6]
    Fact #3, "each face of the octagon will be of identical length; eg, the line segments EF and FG" has been proven.

  8. To determine the internal angle, FZG, we divide it in half by dropping the perpendicular, ZH. ZH has a length of s/2 and FH is half the length of FG, s/2 * (SQRT(2) - 1). This forms a right triangle ZHF with an internal angle FZH and the trigonometric property:
    tan(FZH) = FH / ZH
    tan(FZH) = (s/2 * (SQRT(2) - 1)) / (s/2)
    tan(FZH) = SQRT(2) - 1
    tan(FZH) = 0.414213562373
    FZH = arctan(0.414213562373)
    FZH = 22.5°
    FZG = 2 * FZH
    FZG = 2 * 22.5°
    FZG = 45°
    Fact #2, "the internal angle of each triangle -- eg, the angle FZG -- will be one-eighth of a full circle; ie, 360° / 8 = 45°" has been proven.

  9. By inspection, we see that the octagon is divided into eight isoceles triangles. Each triangle has the same angles and the same length sides. Therefore, they are 8 identical triangles.

    Fact #1, "a regular octagon will contain 8 identical isoceles triangles" has been proven.

All three facts have been proven. Therefore, this puppy is a regular octagon.

QED

Links

My father's sea story was my only source for this method and the basis of this page. But as soon as I had finished writing it I Google'd for construct octagon and found some more. A number of them use circles, but I understand them to be general techniques for constructing n-gons, whereas I believe that my father's method only creates octagons:

Feedback

I had first uploaded this page on 22 Feb 2008. Four months later, I received this email:

Thanks so much!

I need to make a storm cover pane for an octagonal house window, located at some distance, and only measured the flat-to-flat dimension. I figured it would be easy to derive a construction method. Not so! Your method will save the day for me and make me a hero in my wife's eyes.

Thanks again

Glad to have been able to help.

Return to Top of Page
Return to DWise1's Home Page

Contact me.

Share and enjoy!

First uploaded on 2008 February 22.
Updated on 2011 July 08.